小学校も高学年になると『算数が苦手!』という子はいよいよ顕在化してくるものです。
そうした子を見ていると、たいていの場合小3で習う割り算に困難があることがほとんどです。
小4にもなれば、割る数が2桁になったり、小数の割り算があったりと、小3でならう割り算の土台ができていないと太刀打ちできなくなるのは当たり前なのですね。
そして小3で習う割り算は小2で習う掛け算九九がきちんとできていないと、またまた困難になるわけです。
掛け算九九は割り算の土台になるのですね。
ここで多くの人が勘違いしているのが、
掛け算九九ができれば割り算もできる!!
ということです。
掛け算九九ができていても割り算がすぐに出来ない原因
掛け算九九は確かに割り算の土台となりますが、それだけで割り算がスラスラできるようにはなりません。
例えば『54÷6』という計算では、掛け算九九の6の段から答えが54になるときの「かける数」を探して割り算の答えを出します。『6×9=54』の9を探すわけですね。
こうして小3で割り算の答えの出し方を学習するわけです。
大人からすると、『掛け算九九さえ覚えていれば割り算の答えは出せるだろ!』という理屈になりがちです。
まあ理屈はその通りなんですがね。
ただし、小3で
『54÷6』という計算で、掛け算九九の6の段から答えが54になるときの「かける数」は9。だから、『54÷6=9。』
と出すのはそれなりの時間がかかります。
初めて習った段階では、54÷6の答えを出すのに15秒や20秒とそれくらいの時間はかかるのです。
私たち大人は、膨大な経験から54÷6=9など1秒以内で出せるし、長くても5秒以内にはできるでしょう。できない人は知りません。
でも子供は違うのです。特に小3で割り算を習いたての子供は違うのです。
掛け算九九がきちんとできていても15秒はかかると思ってください。
最初はみんなこんな状態です。
さて小学校では3年生のこの状態で、必要な訓練を積まないまま授業は進んでしまいます。
もちろん、24÷6、32÷8といって数十題の計算問題をやらされはします。計算ドリルとかで。
はっきり言いますけど、たかが数十題で割り算はスラスラできるようにはなりません。
24÷6だから、えーと、まずは・・・掛け算九九の6の段から答えが24になるときの「かける数」を探して・・・。えーと、ろくいちが6,ろくにじゅうに、ろくさんじゅうはち、ろくしにじゅうし、あ・・・ろくしにじゅうし、だから4だ!だから『24÷6=4。』
こんな調子でドリルをやるのでしょうが、めちゃくちゃ時間がかかります。
20問でも問題があった日には、途中で飽きること間違いなし。
なんとか時間のかかる割り算のドリルをしのいでも、計算スピードに問題があるまま、3年生を終わるとどうなるか。
4年生以降の割り算は、基本的な割り算を何回も繰り返して解きます。
5241÷3だったら、5÷3、22÷3、14÷3、21÷3と4回の基礎的な割り算をしなければ問題が解けません。
これで基礎的な割り算のスピードに問題があると、5241÷3の1題を解くだけで、2分とか平気でかかるのが一般的です。
さて、こんなのが計算ドリルで20題あったら?
面倒くさすぎて、いよいよ算数嫌い一直線でしょう。
こういうことを防ぐためには、小3で割り算を習った時点で、30÷6といったレベルの問題を1秒以内に解けるようにしなければなりません。
割り算を一瞬で解くために必須!「割り算九九」
とはいうものの何百台という割り算の基礎問題をただ漫然と小3にやらせてもほとんど効果はありません。
ただ数を増やせばいいという問題ではないのです。
ところで、掛け算は「7×8は?」と聞かれて、多くの3年生は3秒以内には「56」と答えられるでしょう。
できないのなら、掛け算九九からやり直しです。
7×8を一瞬で解けるのは、掛け算九九をやったからですね。
耳で問題を聞いて、頭で考える前に答えを口が言ってくれる。反射的に。
そういうレベルまで掛け算九九を体にしみこませたから、すぐに答えられるわけです。
同じことを割り算でもやればいい。
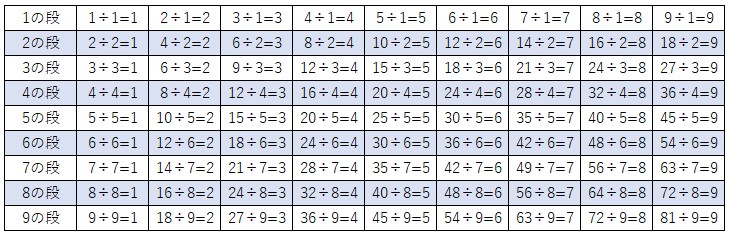
さあ!覚えろ!
とはいうものの、結局は掛け算九九の表と非常に配置が似ていることにそのうち気が付いてきます。
「45は5の段と9の段の数字だ!」くらいまで覚えているといいですね。
当塾ではもっと丁寧に指導しますが、基本的な考えは「割り算もスピードを鍛えないとまるで使い物にならない」ということです。
スピードを鍛えなかったら、算数の伸びは高確率で4年生で止まります。
