「うちの子は全然割合の単元が分かっていない!」という人はとても多い、わかりますよ!
世の中、多くの子が「うちの子は文章題が苦手で・・・」という状況の家庭ばかりなのに、文章題しかない割合の単元が解けるわけがないのですよね。
その結果、中学生にもなっても「くもわ」とかいうわけのわからない公式を使って、結果うまく使えておらず、死屍累々な状況なのです。
とりあえず与えられた数字を適当に「くもわ」に当てはめて、答えを出してみる!みたいな。
パズルじゃないんだけど・・・
「くもわ」を使うにしてもその使い方すら知らないというヤバさ
割合の単元で、よく教えられる「くもわ」って知っていますか?
実は私は大学生になって家庭教師をやるまで知らなかったのです。
そんなものなくても解けるし、それが本質ですから。
でも、学校現場では「くもわ」がないととりあえず答えを出させることができないのでしょうかね。
こういうやつです。
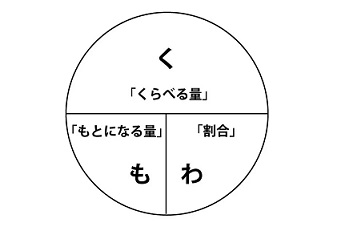
速さで習う「はじき」と似たようなものですが、「はじき」と比べて「くもわ」は公式としては絶望的に使い勝手が悪いのです。それを知らずに「くもわ」を使うのですから、「そりゃ割合を解けないよね」って当たりまえの話なのですよね。
何が違うのかというと、速さで使う「はじき」は速さ・時間・距離のことなのですが、速さの場合は問題文からどれが「速さ」で、どれが「時間」で、どれが「距離」なのか分かりやすいのですよね。
ですから、ただそれを「はじき」に当てはめれば解けるのですよ。
時速80kmで走る電車があります。またA駅からB駅まで200km離れています。この電車がA駅からB駅まで走るとき、何分かかりますか?
上の例題を見ても時速80kmが「速さ」、200kmが「距離」です。文章から見て分かりやすいですよね。
だって「時速」とか、「km」とか、「何分」とか分かりやすい単位が文章にあるので、それを目印にすればいいだけなのです。
あとは「はじき」の公式に当てはめれば、200÷80=2.5時間、よって150分が答えと分かるわけです。
単位変換とかややこしいことはまた別の問題ですが、少なくとも「はじき」に正確に当てはめられないということはないと思います。
多少訓練すれば誰でもできるのですよ。
「はじき」を使う是非は置いておいて・・・。
一方で「くもわ」はどうでしょうか?
「くもわ」の「く」が「比べる量」、「も」が「もとになる量」、「わ」が「割合」なわけです。
もう「比べる量」とかいう言葉が抽象的な時点で結構ヤバイのですがね。
また例題を使いましょう。
ある小学校の5年生の人数は80人で、これは全校生徒の20%にあたります。全校生徒の人数は何人ですか?
これを見てどれが「くらべる量」でどれが「もとになる量」で、どれが「割合」か分かります?
大人は分かるのですよ。経験値が違いますからね。ニュアンスで分かるわけです。
でも子供になんでそれが「もとになる量」になるかきちんと言えますか?
速さの問題のように、文章中のどういう言葉を手掛かりにすればいいのか言えますか?分かりやすく。
まあ「割合」は単位がついていたり、分数だったりするので、わかりやすいのです。「20%」とか「7割」みたいに。
問題は「もとになる量」と「比べる量」なのですよ。
これがどちらか確定できないと、公式に当てはめたところで答えが合わないのは当たり前なのです。
80×20%になるのか80÷20%になるのか、運命を分けるわけです。
こういうことを言うと、必ずこういうことを言う大人がいるのです。
80×20%=16で、これだと全校生徒が16人になってしまう。5年生80人より全校生徒が少ないとかありえないのだから、80÷20%=400で、400人が正解に決まってるだろ。本質的に考えれば分かるはず。これだから塾の先生はすぐテクニックに走って・・・・
そんなこと素人に言われんでもこっちは分かりきっているのです。ですが信じられないかもしれませんが、現実的に半分以上の小学生はそんなことまで頭が回らないのが現実なのですよ。
分数や小数の掛け算・割り算できちんと100点取ってしまうような子でも、上のような理屈に頭が回らず、80×20%とかやってしまうのですよね。
そもそも「くもわ」を使うようなレベルの子というのは、「全校生徒のほうが5年生の人数より多くなければならない」という観点で答えを確かめたりしないのです。
割合を本質的に考えられるのならば「くもわ」なんて使ったりしないのですよね。
こうして先生を中心とした大人に理解されず、割合がわけのわからない状態で適当に「くもわ」に当てはめて「合っていた」「間違っていた」で一喜一憂して終わる小中学生が続出するわけなのですね。
では、どうやって正確に「もとになる量」「くらべる量」を探すのか。
割合の問題があったら真っ先に「もとになる量」を探せ!探し方はこうだ!
先ほど言った通り、問題文の中で「割合」はどれになるか分かりやすい。単位がついていたりするからですね。
ここで詰まる人は「くもわ」以前なので、「割合」とはそもそもなんなのかを学んでください。
さて「割合」が分かれば、あとは「もとになる量」と「比べる量」です。どっちかが分かれば、もう片方は残ったほうなのでどっちかが分かればいいのです。
ですから必ず「もとになる量」を探しましょう。
基本的な探し方はこうです。
「もとになる量」となる言葉は、「割合」の直前に書いてある言葉である。
例えば先ほどの例題をもとに考えてみましょう。
再掲↓。
ある小学校の5年生の人数は80人で、これは全校生徒の20%にあたります。全校生徒の人数は何人ですか?
「割合」の言葉は「20%」ですね。この直前にある言葉は「全校生徒の」です。
ですから「全校生徒」が「もとになる量」なのですね。簡単でしょ?
日本語的にそうならざるを得ないのです。
もちろん例外もあるのですが、小学校レベルの問題の80%はこれで解けるわけです。
国語の文法的に言えば、「割合」を修飾する言葉がなんなのかを見つければいいのですね。
「なんの」20%なのかを見つけ、それが「もとになる量」になるのです。
全校生徒は数字が分かってませんが「もとになる量」です。ですからこれは「もとになる量」を求める問題なのですね。
ついでに「80人」が、残った「比べる量」になるのですね。
ここまでわかればあとは「くもわ」に当てはめて解けばいいのです。
本質的に考えられない子でもこれで、おおむね解けるわけですね。
本質的なところは、「おいおい経験がなんとかしてくれる」でいいじゃないですか。
割合が出来ないことで、算数嫌いを助長するよりはよほどいいはずです。
野球を始めた子供誰もが、「素振りの本質」とか考えて練習しないと思うのですよ。
上手くなる子でも大半は大きくなってから「ああ、素振りで大事なところはこういうところだったんだ」とあとあと気づくものです。
割合の問題の解き方が分かったら練習あるのみ!!
さて、どんなに良い解き方だったとしても練習しなければ全く意味がありません。
最終的に成績を分けるのはそこだったりします。
「分かった」気になるのはやめましょう。
では例題。
①はじめに4800円持っていました。このうち40%を使いました。使った金額は何円ですか。
②折り紙がAの箱の中に12000枚ありました。これはBの箱にある折り紙の枚数の50%にあたります。Bの箱の折り紙は何枚ですか。
③今日はお客さんが27000人来てくれました。昨日は15000人でした。今日のお客さんの人数は昨日のお客さんの人数の何%ですか。
④去年はりんごが2000個取れました。今年は去年の8割しかとれませんでした。今年とれたりんごは何個ですか。
⑤数学のテストで80点とりました。一方で理科のテストは数学の85%の点数をとりました。理科は何点でしたか。
⑥15000人に岸田内閣を応援しているかどうかアンケートをとりました。このうち、30%の人が岸田内閣を応援していました。岸田内閣を応援していない人は何人でしたか。
⑦データによると11歳の男子の体重の平均は39kgで、18歳の男子の体重の平均の65%です。このとき18歳の男子の体重の平均は何kgですか。
⑧A君は200mを20秒で走りました。B君はA君の速さの90%で270m走りました。B君は何秒で270m走りましたか。
さあ解いてください。
まずは「もとになる量」になる言葉を見つけて。
「割合」の直前に書いてある言葉が「もとになる量」でしたね。
では①から
①まず割合が「40%」とあります。この直前の言葉は「このうち」ですね。「このうち」の「この」が何を指しているのかみましょう。「はじめにもっていたお金」つまり4800円のことですね。
ですから、「もとになる量」は4800です。
あとは「くもわ」にあてはめて、
4800×40%=1920
となり、答えは
1920円
②まず割合が「50%」とあります。この直前の言葉は「Bの箱の中にある折り紙の枚数」ですね。ですから「もとになる量」はB箱の折り紙の枚数なのですね。すると残った「Aの箱の折り紙の枚数」の12000が「比べる量」になります。
あとはくもわにあてはめて
12000÷50%=24000
となり、答えは
24000枚
③まず割合は「何%」と分かっていないパターンですね。ですが、「もとになる量」は「割合の言葉の直前に書いてある言葉」という基本は一緒です。よって「何%」の直前に書いてある言葉の「昨日のお客さんの人数」が「もとになる量」で15000人です。そして「比べる量」は残った方の「今日のお客さんの人数」で25000人です。
あとはくもわにあてはめて
27000÷15000=1.8
単位を%に直して、答えは
180%
④まず割合が「8割」と書いてあります。そしてその直前の言葉は「数学の」とありますね。ですから去年とれたりんごが「もとになる量」で2000個です。
あとはくもわにあてはめて
2000×0.8=1600
となり、答えは
1600個
⑤まず割合が「65%」と書いてあります。そしてその直前の言葉は「去年の」とありますね。ですから数学のテストの点数が「もとになる量」で80点です。
あとはくもわにあてはめて
80×0.85=68
となり、答えは
68点
⑥まず割合が「30%」と書いてあります。そしてその直前の言葉は「このうち」とありますね。「このうち」の「この」が何をさすのかというと、「アンケートをやった15000人」のことで、これが「もとになる量」です。
次にくもわにあてはめて
15000×0.3=4500人
となり、岸田内閣を応援している人は4500人です。ですが聞かれているのは「岸田内閣を応援していない人」なので
全体の人数から応援している人を引き算すれば、応援していない人の人数がでます。
15000-4500=10500
となり、答えは
10500人
⑦まず割合が「65%」と書いてあります。そしてその直前の言葉は「18歳の男子の体重の平均の」とありますね。ですから18歳男子の体重平均が「もとになる量」です。一方で残った「11歳の男子の体重の平均」が「比べる量」となり、39kgです
あとはくもわにあてはめて
39÷0.65=60
となり、答えは
60kg
⑧最後は少し難しいです。速さの問題と割合の問題が混ざった話ですね。ちょっとずつひも解いていきましょう。
まず割合が「90%」と書いてあります。そしてその直前の言葉は「A君の速さの」とありますね。ですからA君の速さが「もとになる量」です。
B君の速さが「くらべる量」になりますね。
A君の速さは文章の前半から出せますね。
200mが距離、20秒が時間ですから、
「はじき」にあてはめて
200÷20=10となり、
A君の速さは秒速10mです。これが「もとになる量」ですね。
「もとになる量」と「割合」が分かったので「くもわ」で「比べる量」を出せます。
10×0.9=9
となり、B君の速さは秒速9mとでます。
B君の走った「距離」と、B君の「速さ」が分かったので、「はじき」をつかって「時間」をだせます。
270÷0.9=30
となり、答えは
30秒
ちょっと練習してみましたが、どうでしたか?
毎回「割合の直前の言葉がもとになる量」ということを必ず確認しています。
それがないと解けないからですね。
「くもわ」ばっかり覚えるのではなく、「くもわ」をどう使えばいいのかが大事なのです。
何回も練習しなければ身に付きませんよ!
